Binary Search Tree
검색을 하기위해 유용한 자료구조
배열, 연결리스트 의 경우

앞쪽부터 뒷쪽까지 순차적으로 탐색하기때문에 O(n)
배열로 구현한 이진 탐색의 경우 O(logN)
데이터의 크기가 커질수록 최악과 최선의 경우의 편차가 큼.
이진 탐색 트리

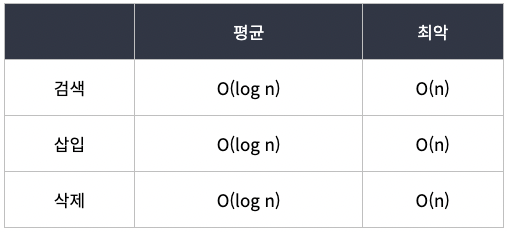
이진 탐색 트리에서 평균적으로 탐색 시간 복잡도는 O(logN) 이다.
최악의 경우

이 경우 O(N)
단점

똑같은 키인 2,3,4,5,6이 들어갔다고해서 이진 탐색 트리의 탐색 시간이 항상 똑같은것은 아니다.
키의 삽입 순서에 따라 트리의 균형이 달라지기 때문에 트리의 균형을 예측하기 어렵다.
크기 순으로 넣으면 불균형해진다.
시간복잡도
이진 탐색 트리의 특징
- 모든 원소의 키는 유일한 키를 가진다.
- 왼쪽 서브 트리 키들은 루트 키보다 작다.
- 오른쪽 서브 트리 키들은 루트 키보다 크다.
- 왼쪽과 오른쪽 서브 트리도 이진 탐색 트리이다.
삽입

삽입은 어렵지 않게 재귀로 구현할 수 있다.
삭제
매우 중요하면서 복잡함
삭제연산은 크게 3가지 케이스로 나눌 수 있다.
- 리프노드를 삭제할 경우
- 자식노드가 한개인 노드를 삭제할 경우
- 자식노드가 두개인 노드를 삭제할 경우
1. 리프 노드를 삭제 할 경우
- 제일 간단한 케이스
- 그냥 연결을 끊어주면 된다.
2. 자식 노드가 하나인 노드를 삭제 할 경우
- 삭제될 노드의 자식노드를 삭제 될 노드의 위치에 승격시킨다.
3. 자식 노드가 두 개인 노드를 삭제 할 경우
- 제일 복잡한 케이스

어떤 노드를 삭제 노드 위치로 가져올 것이냐가 중요하다.
삭제되는 노드와 가장 값이 비슷한 노드를 후계자로 선택해야 이진 탐색 트리가 그대로 유지된다.
그렇다면 가장 값이 가까운 노드란?
- 왼쪽 서브 트리에서 가장 큰 값이나 오른쪽 서브트리에서 가장 작은 값이 삭제되는 노드와 가장 가깝다.
(둘중 아무 거나 사용해도 상관없지만 대부분의 경우에서는 왼쪽 서브트리에서 가장 큰 값을 활용한다)
그런데 한번 스왑했다고 바로 삭제하면 되는것이 아니라
스왑한 이후에도 자식노드가 두개인 경우가 반복적으로 나타날 수 있다.
이럴 경우 전의 과정과 똑같이
삭제할 키와 후계자를 스왑하고,
삭제할 키와 후계자를 스왑하고,
...
를 재귀함수로 반복한다.
그 후
삭제 할 키가
1) 리프 노드가 되었을 때
2) 자식 노드가 하나인 노드가 되었을 때
즉, 1)번조건이나 2)번조건을 만족하였을 때 그 키를 비로소 삭제 한다.

(1)삭제할키는 12이다.
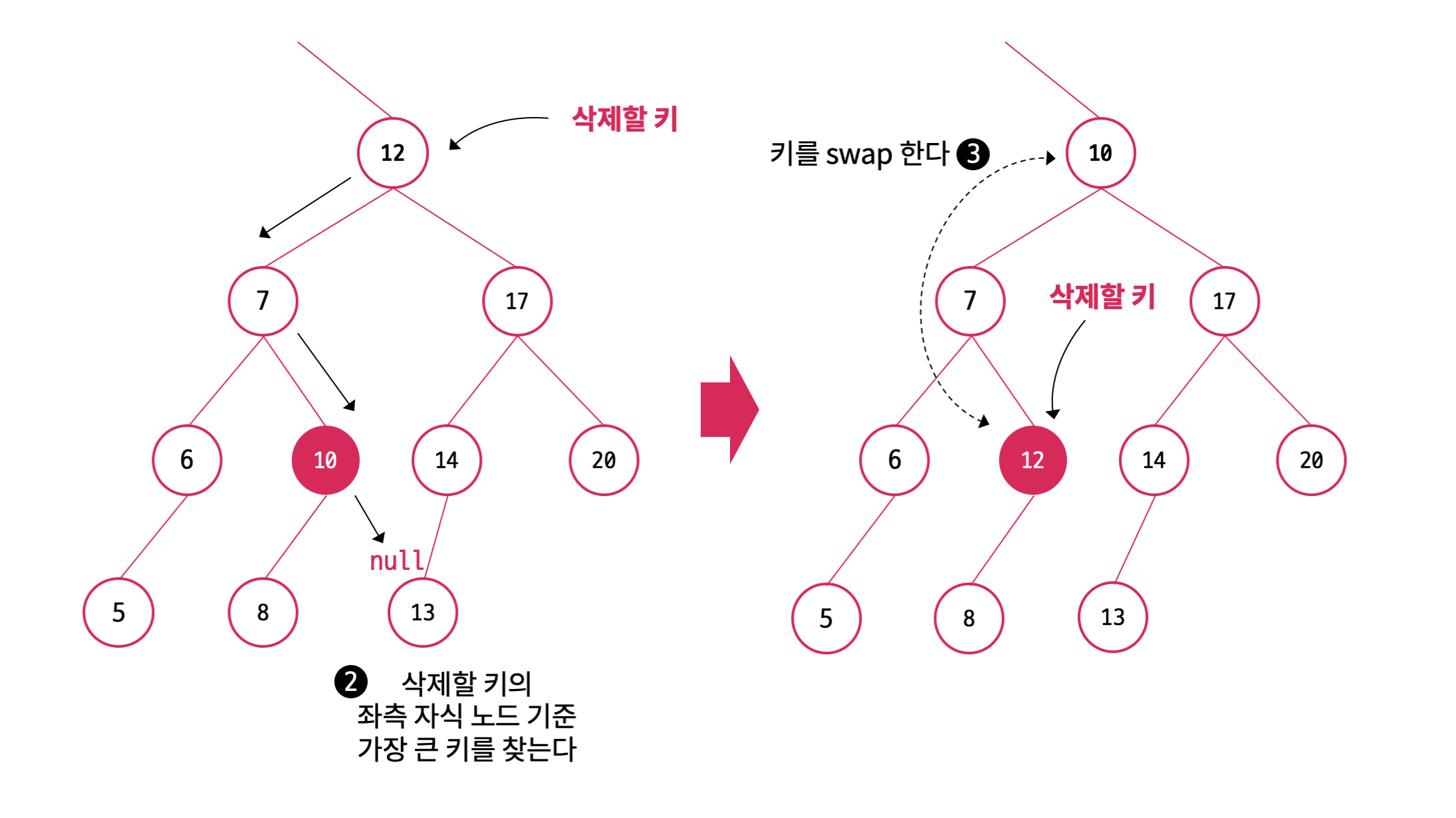
(2)12의 좌측노드에서 가장큰 키인 10과 swap

삭제할키는 2번조건인
2)자식노드가 하나인 노드
를 만족하게 되었으므로,
2번 조건에따라 삭제한다.
'PS > 자료구조' 카테고리의 다른 글
| [Java] 힙 (Heap) , 우선순위 큐(Priority Queue) (0) | 2022.08.02 |
|---|---|
| [Java] 그래프 (Graph) (0) | 2022.07.25 |
| [SWEA] 1248. 공통 조상[Java] (0) | 2022.07.24 |
| [SWEA] 1233. 사칙연산 유효성 검사 [Java] (1) | 2022.07.24 |
| [SWEA] 1232. 사칙연산 [Java] (0) | 2022.07.24 |