그래프
- 그래프는 정점(Vertex)들의 집합과 이들을 연결하는 간선(Edge) 들의 집합으로 구성된 자료구조 형태
- 선형 구조나 트리 형태로 나타내기 어려운 N:N 관계를 가지는 원소들의 표현에 적합하다.
그래프 유형
- 무향 그래프(Undirected Graph)
- 유향 그래프(Directed Graph)
- 가중치 그래프(Weighted Graph)
- 사이클 없는 방향 그래프(DAG, Directed Acyclic Graph)
- 완전 그래프 (정점들에 대한 모든 간선이 존재하는 그래프)
- 부분 그래프 (원래의 그래프에서 일부의 정점이나 간선만 나타낸 그래프)
인접하다 (Adjacency)
- 두개의 정점에 간선이 존재 하면 두 정점은 인접해 있다.
- 완전 그래프는 임의의 정점 V1,V2가 모두 인접해 있다.
경로
- 단순경로
- 경로 중 한 정점을 최대 한번만 지나는 경로를 단순 경로 라고 한다 (1-4-6-7) - 사이클
- 시작한 정점에서 끝나는 경로를 사이클이라고 한다. (1-4-6-7-1)
성질
- 무향 그래프에서 |V| 개의 정점을 가지는 그래프의 최대 간선은 |V| * |V - 1| / 2
- 유향 그래프에서|V| 개의 정점을 가지는 그래프의 최대 간선은 |V| * |V - 1|
그래프의 표현
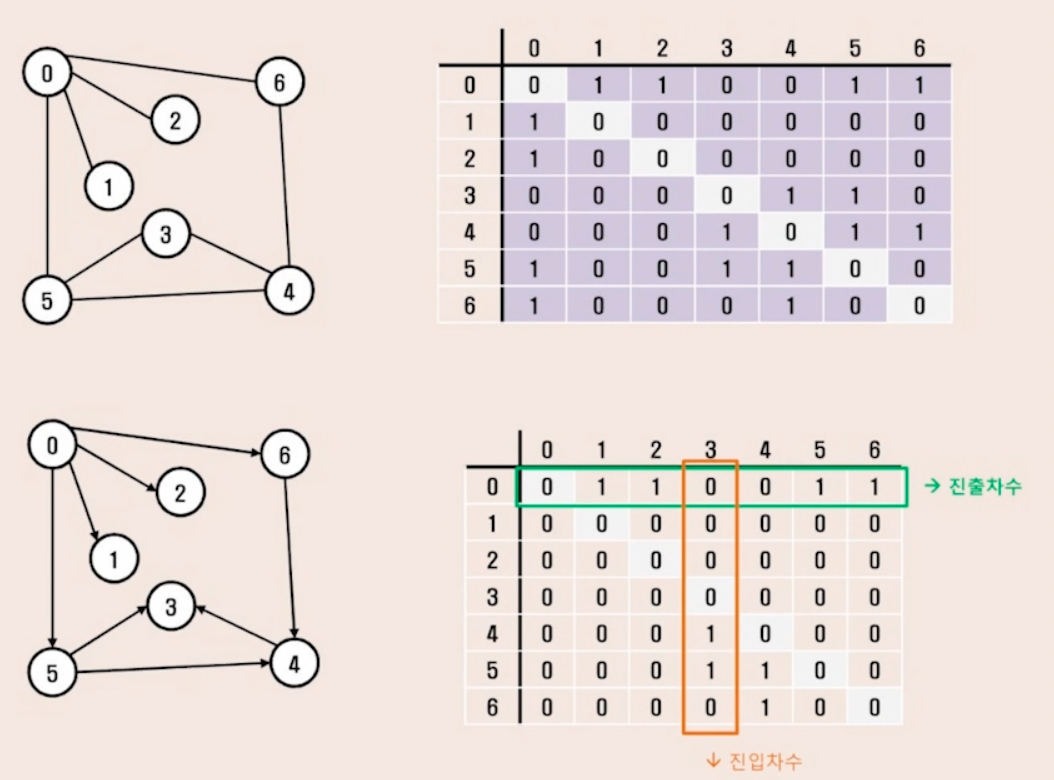
1. 인접 행렬(Adjacent Matrix)
|V| * |V| 크기의 2차원 배열을 사용해서 간선 정보를 저장
1.인접 행렬(Adjacent Matrix)
|V| * |V| 크기의 2차원 배열을 사용해서 간선 정보를 저장
- 각 정점마다 해당 정점으로 나가는 간선의 정보를 저장
- 두 정점이 연결되어 있으면 1 , 연결되어 있지 않으면 0 을 저장 (가중치 그래프에서는 가중치를 저장)
- 무향 그래프에서 i번째 행의 합 = i번째 열의 합 = Vi의 차수
- 유향 그래프에서 i번째 행의 합 = Vi의 진출 차수
i번째 열의 합 = Vi의 진입 차수
2.인접 리스트(Adjacent List)
그래프의 간선 정보를 리스트에 담아 저장

인접 행렬 vs 인접 리스트?
인접 행렬의 장점
1. 구현 하기 쉽다
2. 탐색 하는데 빠른 시간이 걸린다
(1,5사이의 간선이 있는지 확인하려면 m[1][5]를 체크해주기만 하면 됨)
인접 행렬의 단점
1. |V|*|V|크기의 행렬을 만들기 때문에 불필요한 메모리의 사용이 있다.
인접 리스트의 장점
1. 존재하는 간선들만 저장하기때문에 메모리의 효율적 사용이 가능하다.
인접 리스트의 단점
1. 행렬을 탐색하는 과정에서 시간이 많이 소요된다.
(1,5 사이의 간선이 있는지 확인하려면 V[1]의 모든 리스트들을 탐색해야한다.
'PS > 자료구조' 카테고리의 다른 글
| [SWEA] 3000. 중간값 구하기 [Java] (0) | 2022.08.09 |
|---|---|
| [Java] 힙 (Heap) , 우선순위 큐(Priority Queue) (0) | 2022.08.02 |
| [Java] 이진 탐색 트리 (Binary Search Tree) (0) | 2022.07.24 |
| [SWEA] 1248. 공통 조상[Java] (0) | 2022.07.24 |
| [SWEA] 1233. 사칙연산 유효성 검사 [Java] (1) | 2022.07.24 |